ml►a-algorithm

ml-a02-multiple_linear_regression

Multiple Linear Regression

1
2
3
4
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
1
2
data = genfromtxt(r"Delivery.csv", delimiter=",")
print(data)
[[100.    4.    9.3]
 [ 50.    3.    4.8]
 [100.    4.    8.9]
 [100.    2.    6.5]
 [ 50.    2.    4.2]
 [ 80.    2.    6.2]
 [ 75.    3.    7.4]
 [ 65.    4.    6. ]
 [ 90.    3.    7.6]
 [ 90.    2.    6.1]]

1
2
3
4
5
6
# all data until the last column
x_data = data[:, :-1]
# label: the last column
y_data = data[:, -1]
print(x_data)
print(y_data)
[[100.   4.]
 [ 50.   3.]
 [100.   4.]
 [100.   2.]
 [ 50.   2.]
 [ 80.   2.]
 [ 75.   3.]
 [ 65.   4.]
 [ 90.   3.]
 [ 90.   2.]]
[9.3 4.8 8.9 6.5 4.2 6.2 7.4 6.  7.6 6.1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def compute_error(theta0, theta1, theta2, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (theta1 * x_data[i, 0] + theta2 * x_data[i, 1] + theta0))**2
    return totalError / float(len(x_data))

def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
    # total data number
    m = float(len(x_data))
    for i in range(epochs):
        theta0_grad = 0
        theta1_grad = 0
        theta2_grad = 0
        for j in range(0, len(x_data)):
            theta0_grad += (1/m) * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
            theta1_grad += (1/m) * x_data[j, 0] * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
            theta2_grad += (1/m) * x_data[j, 1] * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
        theta0 = theta0 - (lr * theta0_grad)
        theta1 = theta1 - (lr * theta1_grad)
        theta2 = theta2 - (lr * theta2_grad)
    return theta0, theta1, theta2
1
2
3
4
5
6
7
8
9
10
11
12
lr = 0.0001
theta0 = 0
theta1 = 0
theta2 = 0
epochs = 1000
print("starting theta0={0}, theta1={1}, theta2={2}, error={3}"
      .format( theta0,theta1,theta2,compute_error(theta0, theta1, theta2, x_data, y_data)))
print("Running...")
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)
print("After {0} iterations theta0={1}, theta1={2}, theta2={3}, error={4}"
      .format( epochs, theta0,theta1,theta2,compute_error(theta0, theta1, theta2, x_data, y_data)))    
      
starting theta0=0, theta1=0, theta2=0, error=47.279999999999994
Running...
After 1000 iterations theta0=0.006971416196678632, theta1=0.08021042690771771, theta2=0.07611036240566814, error=0.7731271432218118

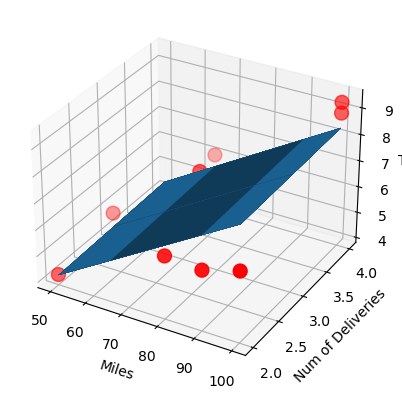
1
2
3
4
5
6
7
8
9
10
11
12
13
14
ax = plt.figure().add_subplot(111, projection="3d")
# c='r' => red color, marker='o' => use o to print the figure, s=100 => the marker size is 100
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c='r', marker="o", s=100)

x0 = x_data[:, 0]
x1 = x_data[:, 1]
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + theta1 * x0 + theta1 * x1
ax.plot_surface(x0, x1, z)

ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')
plt.show()

PS:
Delivery.csv

Sklearn

1
2
3
4
5
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from sklearn import linear_model
from mpl_toolkits.mplot3d import Axes3D
1
2
data = genfromtxt(r"Delivery.csv", delimiter=",")
print(data)
[[100.    4.    9.3]
 [ 50.    3.    4.8]
 [100.    4.    8.9]
 [100.    2.    6.5]
 [ 50.    2.    4.2]
 [ 80.    2.    6.2]
 [ 75.    3.    7.4]
 [ 65.    4.    6. ]
 [ 90.    3.    7.6]
 [ 90.    2.    6.1]]

1
2
3
4
5
6
# all data until the last column
x_data = data[:, :-1]
# label: the last column
y_data = data[:, -1]
print(x_data)
print(y_data)
[[100.   4.]
 [ 50.   3.]
 [100.   4.]
 [100.   2.]
 [ 50.   2.]
 [ 80.   2.]
 [ 75.   3.]
 [ 65.   4.]
 [ 90.   3.]
 [ 90.   2.]]
[9.3 4.8 8.9 6.5 4.2 6.2 7.4 6.  7.6 6.1]

1
2
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
LinearRegression()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
1
2
3
4
5
6
print("coefficients:", model.coef_)
print("intercept:", model.intercept_)

x_test = [[102,4]]
predict = model.predict(x_test)
print("predict:", predict)
coefficients: [0.0611346  0.92342537]
intercept: -0.868701466781709
predict: [9.06072908]

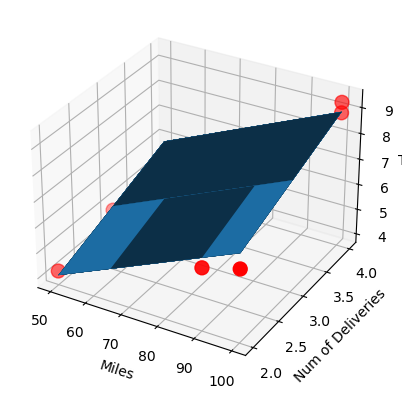
1
2
3
4
5
6
7
8
9
10
11
12
13
14
ax = plt.figure().add_subplot(111, projection="3d")
ax.scatter(x_data[:,0], x_data[:,1], y_data, c='r', marker='o', s=100)
x0 = x_data[:,0]
x1 = x_data[:,1]
x0,x1 = np.meshgrid(x0,x1)

z = model.intercept_ + x0*model.coef_[0] + x1*model.coef_[1]

ax.plot_surface(x0, x1, z)
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')

plt.show()